
Байгаль ертөнц дээр янз бүрийн зангилаануудыг харж болно. Тэдгээрийн зарим нь гоёл чимэглэл мэт харагдавч үнэндээ нарийн төвөгтэй математик объектууд юм. ᠌᠌᠌᠌“Зангилааны онол” гэсэн математик салбар эдгээр зангилааг судлахад зориулагдсан байдаг. Ердийн нэг зангилааны сул үзүүрийг өөр нэг зангилааны үзүүртэй холбоход шинэ математик зангилаа бий болно.
Математикчид хэрэв хоёр өөр хэсэг зангилааны зүссэн үзүүрийг хооронд нь холбоход үүссэн шинэ зангилаа тус бүрийн нарийн төвөгтэй байдлын нийлбэртэй адил нарийн төвөгтэй болно гэж эртнээс итгэдэг байсан. Гэвч судлаачид саяхан хэсгүүдийн нийлбэрээс илүү энгийн зангилааг олж илрүүлжээ.
Зангилааны онол нь топологийн нэг салбар бөгөөд уураг, молекулын бүтцийг хэрхэн тогтвортой байдгийг ойлгох гэх мэтэд практик хэрэглээтэй байдаг. Гол асуудал нь аль зангилаа өвөрмөц ялгаатай эсвэл аль зангилаа бусадтай ижил болохыг хэрхэн мэдэх вэ гэдэгт байдаг.
Хэрэв нэг зангилааг өөр зангилаатай ижил болгохын тулд таслах шаардлагүй, зөвхөн татах мушгих, сунгах байдлаар хувиргаж болдог бол ижил зангилаанууд болох ба зангилааны утсыг зүсэж, дахин холбох шаардлагатай бол ялгаатай зангилаанууд болно. Эдгээр үйлдлүүдийг ашиглан математикчид эдгээр зангилаануудыг ᠌᠌ “сулруулах тоо” буюу “unknotting number” гэсэн үзүүлэлтээр хэмжинэ. Энэ нь тухайн зангилааг хамгийн энгийн хэлбэрт хувиргахын тулд хэдэн удаа зүсэж, хэдэн удаа холбох шаардлагатайг илэрхийлнэ. Гэвч энэ тоог олох нь маш хүнд бодлого юм.
Хэрэв хоёр жижиг зангилааг нийлүүлж нэг том зангилаа үүсгэвэл үүнийг тайлах хамгийн хурдаг арга нь тус тусын хэсгүүдийг салангид тайлах үйлдлийн тоотой тэнцүү байх ёстой гэсэн таамаглалт олон математикчид итгэж байв. Энэ санааг 1937 онд Хилмар Вендт (Hilmar Wendt) таамаг хэлбэрээр дэвшүүлсэн ба бараг зуун жилийн турш батлагдаагүй хэвээр байв.
“Саяхныг болтол энэ таамаглалыг батлах тодорхой арга байгаагүй. Гэхдээ одоо худал болохыг тогтоосон” гэж Небраска-Линкольны Их Сургууль (University of Nebraska-Lincoln)- н математикч Марк Бриттенхэм ᠌(Mark Brittenham) хэлжээ.
Бриттенхэм болон хамтран зохиогч Сюзан Хермиллер ᠌(Susan Hermiller) (мөн Небраска-Линкольны Их Сургууль ) нарын arXiv.org-д байршуулсан судалгаанд хоёр зангилааг холбосноор үүсэх шинэ зангилаа нь хүлээгдэж байснаас хамаагүй бага алхмаар тайлагдаж болохыг харуулжээ. Тэд сулруулах тоо нь гурван алхамтай зангилааг түүний толь дүрстэй холбож илүү том зангилаа үүсгэсэн байна. Онолын дагуу уг зангилааг тайлахад зургаан алхам шаардагдах байсан ч бодит байдалд таван алхам, магадгүй бүр цөөн алхмаар тайлагдаж болохыг тогтоожээ.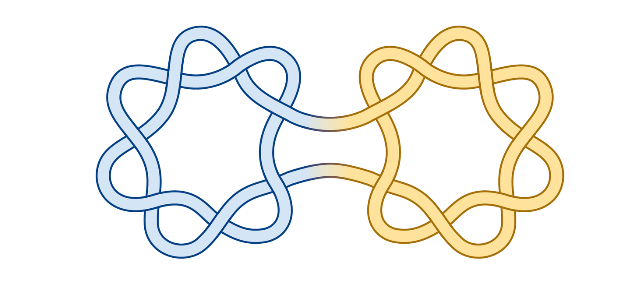
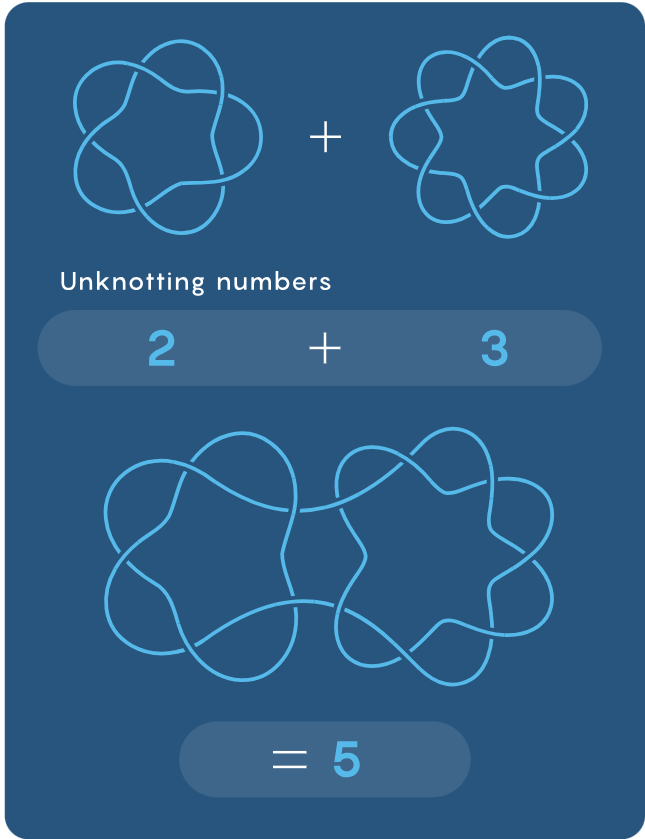
Энэ бол маш гайхамшигтай зүйл. Энэ бидний зангилааны төвөгшлийн талаарх ойлголтод асуудал байж болохыг харуулж байна хэмээн Рутгерс их сургууль(Rutgers University)- н математикч Кристен Хендрикс (Kristen Hedricks) (судалгаанд оролцоогүй) хэлжээ.
Эх сурвалж
Мэдээ бэлтгэсэн ЭША Ж.Даваажаргал