
Квант тооцоолол нь зөвхөн онолын физикчид эсвэл программ хангамжийн инженерүүдэд зориулагдаагүй бөгөөд энэ нь санхүүгийн салбарт мөн цоо шинэ боломжийг нээж өгч байна.
Аливаа систем нь хэмжилт хийгдэх хүртэл бүх боломжит төлөвүүдийн давхцал (суперпозиц) дотор оршдог гэж 1935 онд физикч Эрвин Шрёдингер тодорхойлсон. Шрёдингерийн муур нь радиоактив атом, Гейгер тоолуур, алх, хорт бодистой хамт хайрцагт байрлуулагддаг бөгөөд хайрцгийг онгойлгох хүртэл амьд ч байж болно, үхсэн ч байж болно, өөрөөр хэлбэл хоёр төлөвт зэрэгцэн оршдог. Математик хэллэгээр бол Шрёдингерийн муурын төлөвийг bra-ket тэмдэглэгээгээр дараах байдлаар илэрхийлж болно:
|Муур⟩ = √(1-p) |Амьд⟩ + √p |Үхсэн⟩
Энд p нь радиоактив задралын магадлал юм. Хэрэв бид муурыг 50 настай Alice хэмээх амь насны даатгуулагч гэж үзвэл томьёо дараах хэлбэртэй болно:
|Alice⟩ = √(1-q50) |Амьд⟩ + √q50 |Үхсэн⟩
Энд q50 нь 50 нас хүрсэн хүн 51 нас хүрэхээсээ өмнө нас барах магадлал(актуарууд болон хүн ам зүйчдийн ашигладаг амьдралын хүснэгтэд байдаг) юм. Квант гэдгийн ард энгийн бином тархалт оршдог. Шрёдингерийн хайрцаг нь эцэстээ квантын хэлбэртэй илэрч байгаа жирийн актуарийн эрсдэлийн тусгал болж болно.
Бид ихэнхдээ санамсаргүй тоо үүсгэгчүүдийг (жишээлбэл Excel-ийн ‘RAND()’ функц) жинхэнэ санамсаргүй байдал үүсгэдэг мэтээр хүлээн зөвшөөрдөг ч, энэ нь тухайн тодорхойлогдсон эх тооноос давтагддаг хуурамч санамсаргүй (pseudo-random) тоо үүсгэгч механизм юм. Нэг магадлалын утгыг double precision форматаар хадгалахад 64 бит шаардлагатай байдаг бол, RAND() функцэд ашиглагддаг Mersenne Twister алгоритмыг ажиллуулах дотоод системд 20,000 бит хэрэгтэй байдаг. Хуурамч санамсаргүй тоонуудад тулгуурладаг уламжлалт симуляциас ялгаатай нь, квант тооцоолол нь магадлалуудыг (жишээлбэл, нас баралтын хувь) байгалиасаа квант битүүдэд (qubit) шингээдэг бөгөөд санамсаргүй байдал нь квант физикийн үндсэн хэсэг юм.
Магадлалуудыг квант битэд хэрхэн кодолж болохыг харвал, Alice-ийн төлөвийг дараах байдлаар ерөнхийлөн илэрхийлнэ:
|Ψ⟩ = cos(θ/2) |0⟩ + e^(i*φ) sin(θ/2) |1⟩
Bloch бөмбөрцгүүд (Зураг 1) нь квант битийн төлөвийг геометрээр дүрслэн харуулах боломжийг олгодог. Ямар ч квант төлөвийг энэ бөмбөрцгийн гадаргуу дээрх нэг цэгээр илэрхийлж болох бөгөөд хоёр өнцгөөр (θ ба φ) тодорхойлно. Энэ нь газрын уртраг, өргөргийг зааж буйтай адил юм. Эдгээр өнцгүүдийг тохируулснаар (sin(θ/2) = √p), магадлалуудыг (q50) шууд квант төлөвт кодлох боломжтой. Энэ нь зүгээр нэг “зооc хаях” жишээнээс хэтэрч, хоёр туйлын оронд бүхэл бүтэн бөмбөрцгийн боломжийг ашиглаж байна гэсэн үг юм. Үүнийг бид Python хэл дээр Qiskit багцыг ашиглан хялбархан хэрэгжүүлж чадна (Зураг 2).
Зураг 1: Bloch бөмбөрцгүүд. Qubit-ийн квант төлөвийн геометр дүрслэл.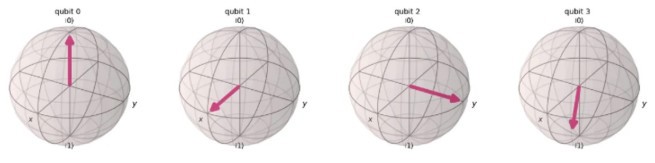
Зураг 2: Магадлалыг Qubit-руу кодлох
Зураг 2-ын зүүн гар талын эхний хэсэг бол ямар ч хувиргалт хийгдээгүй байх үеийн квант битийн анхны төлөв буюу хойд туйлд байрлах ∣0⟩ төлөв. Дунд хэсэгт 0.3 гэсэн магадлалыг хэрхэн кодолж байгааг харуулсан ба дээр дурдсан тригонометрийн хамаарлыг ашиглан y-тэнхлэгийн дагуу эргүүлэх үйлдэл хийсэн (x-тэнхлэгээр эргүүлэх ч мөн боломжтой). Эцэст нь, квант битийг 10,000 удаа хэмжсэний үр дүнд үүсэх магадлалын тархалтыг харууллаа. Үүний үр дүнд ∣1⟩ төлөв ажиглагдах магадлал ойролцоогоор 30% болж байгаа нь бидний кодолсон утгатай нийцэж байна.
Энтанглед амь нас
Нэг кубитыг хэмжихэд нөгөө кубитын төлөв тодорхой болж байх шинж чанарыг квант энтанглемент гэнэ. Альберт Эйнштейн үүнийг“хол зайнаас хий үзэгдэл мэт үйлчлэх нөлөө” хэмээн хэлсэн байдаг.
Bob (|0⟩) бол 90% амьд үлдэх магадлалтай (qx = 0.1), харин Alice (|1⟩) бол 95% амьд үлдэх магадлалтай (qx = 0.05) гэж үзье. Тэдний хамтын магадлалын тархалт нь тус бүрийн магадлалын үржвэрээр тооцоологдоно.
Зураг 3-т q0 нь Bob-ыг, q1 нь Alice-ийг төлөөлж байгаа. Bloch бөмбөрцгүүд нь энэ хоёрын квант битэд кодлогдсон амьд үлдэх (эсвэл нас барах) магадлалуудыг үзүүлсэн бол гистограмм график нь хэмжилтийн үр дүнг харуулсан. Үүссэн магадлалын тархалт нь, хэрэв Bob ба Alice бие даасан гэж үзвэл, хамтын магадлалын тархалтыг харуулж байна.
Зураг 3: Магадлалыг Qubit-руу кодлох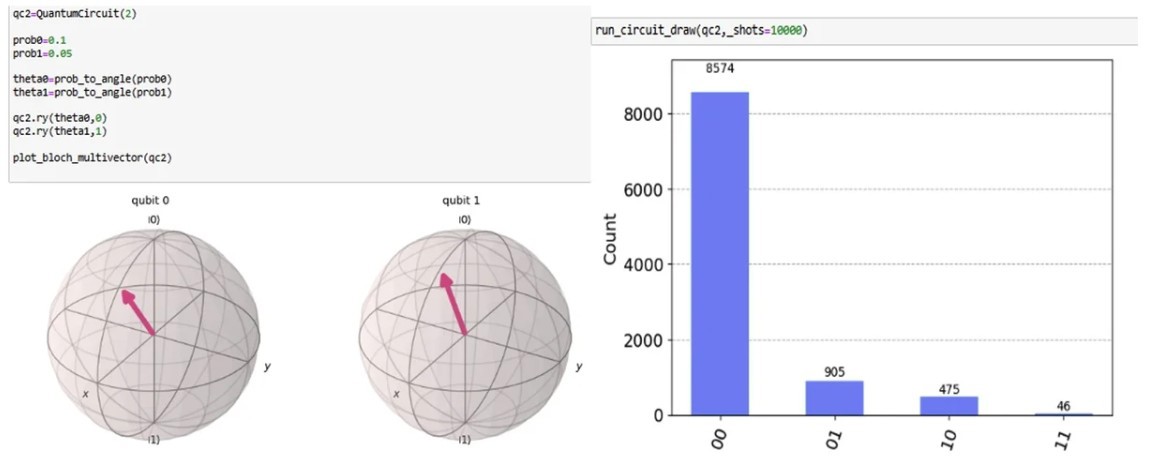
Bob болон Alice нар гэрлэж тэдний ирээдүй нь хоорондоо хамааралтай болсон гэж үзье. Тэдний нас баралтын хувь тус тусдаа 0.1 ба 0.05 хэвээр үлдэх ч, хэрвээ Bob нас барвал, үүнээс үүдэлтэй Alice-ийн үхэх нөхцөлт магадлал магадгүй гашуудлаас ч юм уу бусад хамаарал бүхий хүчин зүйлээс шалтгаалж 50% болно. Энэ нь мөн (Байесын теоремоор) Bob хэзээ ч Alice-аас илүү наслахгүй гэсэн дүгнэлтэд хүрнэ.
Кубитүүдийн төлөвийг өөрчлөхдөө дараалсан үйлдлүүд хийдэг бөгөөд энэ үйл явцыг квант схем гэнэ. Зураг 4-д Alice болон Bob-ыг тус бүр нэг нэг кубитээр (q0 ба q1) илэрхийлсэн ба тэдгээрийн хоорондын хамаарлыг y тэнхлэгийн дагуу (хяналттайгаар) эргүүлж дүрслэн үзүүлжээ. Энэ нь Bob-ын кубитийн төлөвт үндэслэн Alice-ийн кубитийг нөхцөлтэйгөөр хувиргахыг харуулж буй юм.
Зураг 4: Bob болон Alice-ийн үхлийн хамаарлын магадлалыг харуулсан квант схем.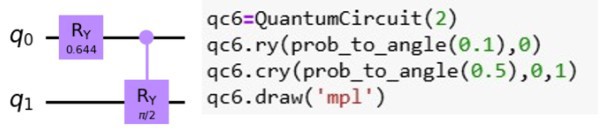
Зураг 5: Зураг 4-ийг графикт харуулав.
Онолын таамаглал Квант төхөөрөмжийн үр дүн
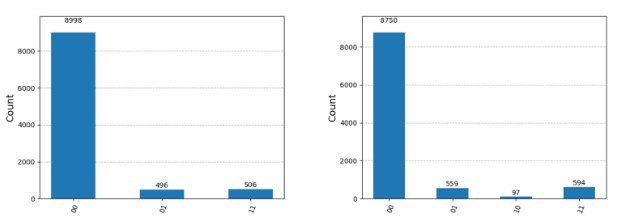
Зураг 5-ын симуляцийн үр дүн:
|00⟩ = 0.9 (хоёулаа амьд)
|01⟩ = 0.05 (Bob нас барж, Alice амьд)
|11⟩ = 0.05 (хоёулаа нас барсан, P(A|B = 0.5)
Зураг 5-д үзүүлсэн квант төхөөрөмжийн үр дүн нь онолын таамаглалтай бага зэрэг зөрж байгаа нь өнөөгийн квант тооцооллын төгс биш, дутагдалтай талтай холбоотой. Бидний гэрлэсэн хосуудын зүйрлэлээр бол, Bob заримдаа Alice-аас урт насалж байна (|10⟩ = 0.0097). Энэ нь онолын нөхцөлд гарч ирдэггүй үр дүн юм.
Суперпозици ба энтанглемент нь кубитүүдэд бүхэл бүтэн магадлалын тархалтыг маш үр ашигтайгаар кодлох боломжийг олгодог. Бид зөвхөн хоёр кубит ашигласнаар санамсаргүй тоо үүсгэж, магадлалыг кодолж, нөхцөлт логик зэргийг хэрэглэн уламжлалт аргаар хэдэн арван мянган бит шаардлагатай тооцоог хийж чадлаа. Энэ давуу тал нь асуудлын цар хүрээ нэмэгдэх тусам хадгалагдсаар байдаг ба бүх амьдралын хугацааг хамарсан тооцоог ердөө долоон кубитээр гүйцэтгэж болно.
Зураг 6 нь Bloch бөмбөрцөг дээр 104 ширхэг нас баралтын цэгийг харуулсан бөгөөд эдгээр кубитийг давтан хэмжих замаар гарч ирж буй нийт тархалтыг мөн дүрслэн харуулж байна. Энэ нь одоогоор мэдэгдэж буй AMC00-ийн утгуудыг маш өчүүхэн хэмжээний өгөгдлийн хадгалалт ашиглан ойролцоогоор тооцоолж буй хэрэг юм. (AMC00 гэдэг нь эрэгтэйчүүдийн дундаж нас барах магадлалыг насны ангиллаар харуулсан хүснэгт юм.)
Зураг 6: 7 кубитэд кодлогдсон AMC00

Deutsch-ийн тэтгэвэр
Британийн физикч Дэвид Дойч нь Шорын үржвэрийг задлах аргыг “зэрэгцээ орчлонгууд” хамтдаа оршиж байгаа мэтээр зүйрлэсэн бөгөөд энэ санаа нь мөн квант схем ашиглан тэтгэврийн үнэлгээ хийхэд хэрэглэдэr болно. Үндсэн арга нь дараах байдалтай байна:
Энгийн дөрвөн жилийн жишээг авч үзье:
Тэтгэвэр авдаг хүн хамгийн ихдээ дөрвөн жил амьдрах боломжтой бөгөөд магадлалууд нь Dₓ = [0.1, 0.2, 0.3, 0.4] гэж өгөгджээ. Төлбөрүүд нь жил бүр урьдчилан (0, 1, 2 ба 3-р жилүүдэд) хийгдэнэ.
Эхний хоёр кубит (q0, q1) нь тархалтыг илэрхийлнэ, харин гурав дахь кубит (q₂) нь хэдэн төлбөр хийгдсэнийг.хянаж.тоолно.
Хяналттай хувиргалтууд нь q0 ба q1-ийн суурь төлөв бүр дээр үндэслэн q₂-г “идэвхжүүлнэ” (жишээ нь, суурь төлөв |00⟩ байвал тэтгэвэр авагч нь эхний жилдээ нас барсан гэж үзнэ, тиймээс хувиргалт нь зөвхөн нэг удаагийн төлбөрийг кодолно).
Зураг 7 нь энэхүү квант гүйцэтгэлийг харуулсан. Энэхүү зураг нь логикийг тодорхой болгохын тулд дараах 3 үндсэн хэсэгт хуваагдсан:
Хамгийн зүүн хэсэг дэх (нил ягаанаар тодруулсан), q0 ба q1 кубитүүд дээрх Ry хувиргалтууд нь нас баралтын тархалт болох Dₓ = [0.1, 0.2, 0.3, 0.4]-ийг кодолсон.
Эдгээр дарааллын ээлж бүр нь тухайн өгөгдсөн жилд тэтгэвэр авагчийн нас барах магадлалыг кубитийн магадлалын далайцтай тохируулдаг.
Дунд буй дөрвөн хэсэгт X хувиргалтууд нь (номин цэнхэр өнгөтэй) q0 ба q1 кубитүүдийг шаардлагатай үед эргүүлж, хяналттай Ry хувиргалтуудыг өдөөж, q2 дээр идэвхжүүлж байна.
Эдгээр хэсэг бүр нь байж болох төлбөрүүдийн аль нэгтэй (1-ээс 4 хүртэл) харьяалалтай байна. Хэрэв тухайн төлөв нь тэтгэвэр авагч амьд байгааг илэрхийлж байвал, q2-ийн далайц дээр тухайн төлбөр нэмэгдэнэ.
Сүүлийн хэсэгт бид q2 буюу “төлбөрийн” кубитийг хэмжинэ.
Зураг 7: 4 жилийн хувьд тэтгэврийн үнэлгээг харуулсан квант схем

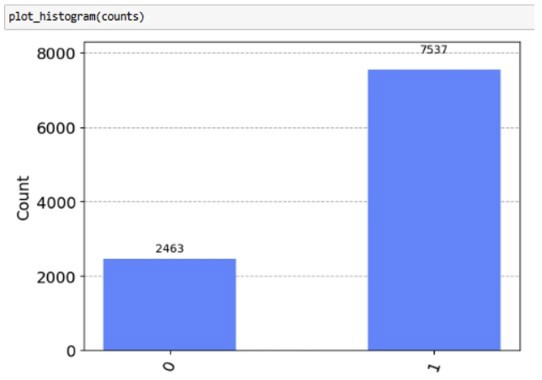
Зураг 8-д q2–ийн хэмжилтийн ойролцоогоор 75% нь ∣1⟩ байсныг харуулсан. Бүх 4 төлбөрийг 0.75-аар үржүүлэх нь хүлээгдэж буй төлбөрийг 3 гэсэн үр дүнд хүргэж байна. Үүнийг уламжлалт тооцооллоор харуулбал 0.1×1+0.2×2+0.3×3+0.4×4=3 ийм болно.
Зураг 8: Зураг 7-д буй квант схемийг ажиллуулсан үр дүнг графикаар харуулав.
Энэхүү хэрэгжилтийг хялбархан өргөтгөж, ердөө найман кубитээр бүтэн амьдралын турш дахь хувилбарыг хийх боломжтой. 7 кубит нь Dₓ-ийг кодлоход, нэг кубит нь “төлбөр”-ийг кодлох ба хэмжихэд ашиглагдана гэсэн үг.
Зураг 9-д Qiskit (Python)-ийг ашиглан 60 настай хүний хувьд, мөн тогтмол 2% хүүтэй тохиолдолд үр дүнг харуулсан. 60-аас 120 насны хүмүүсийн хувьд амьд үлдэх магадлалуудыг кодлоход ердөө зургаан кубит хэрэгтэй бөгөөд долоо дахь кубит нь хяналттай хувиргалтууд болон хэмжилтэд зориулагдана. Тэтгэврийн төлбөр нь жил бүр урьдчилан төлөгддөг гэж үзвэл, онолын хувьд зөв утга нь 17.735 байна. Бидний квант үр дүн үүнд нэлээд ойртсон. Гэхдээ квант процессын магадлалын шинж чанараас шалтгаалан схемийг ажиллуулах бүрт бага зэрэг хэлбэлзэл ажиглагддаг. Классик, хуурамч санамсаргүй үүсгэгчүүдээс ялгаатай нь, квант санамсаргүй үзэгдлийг програмчлах боломжгүй тул ийм зөрүү гардаг. Үр дүнгийн нарийвчлалыг сайжруулахын тулд, схемээс загвар авах давталтын тоог нэмэгдүүлэх боломжтой.
Зураг 9: Эцсийн кубитийг хэмжих замаар Qiskit ашиглан тэтгэврийг үнэлэх.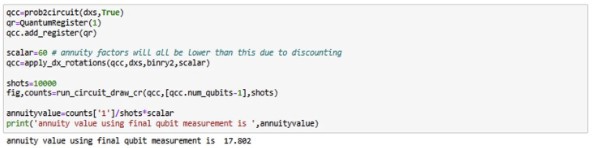
Энэ арга нь цөөн тооны даатгуулагчтай тохиолдолд үр дүнтэй ажилдаг. Үр дүнг сайжруулахын тулд загвар авах давтамжийг нэмэгдүүлэх нь хэдэн зуун мянган даатгуулагч бүхий бодит багцтай үед практик бус бөгөөд их хэмжээний нөөц, бололцоо шаардана. Үүний оронд бид квант далайцын үнэлгээ (QAE)-г ашиглаж болно. QAE нь “хэмжилтийн кубит” |1⟩ төлөвт байх магадлалыг үнэлэх зориулалттай квант алгоритм юм. QAE нь квадрат хурдатгалыг ашигладаг бөгөөд үнэлгээний тодорхойгүй байдал нь уламжлалт Монте Карлогийн 1/√N-тай харьцуулахад 1/N-тэй пропорциональ байдаг.
Зураг 10 нь QAE-ийг Qiskit ашиглан гүйцэтгэж байгаа бөгөөд оновчтой тэтгэврийн үнэлгээг тогтооход нарийвчлал сайтай байгаа нь харагдаж байна.
Зураг 10: QAE ашиглан тэтгэврийг үнэлгээг сайжруулсан байдал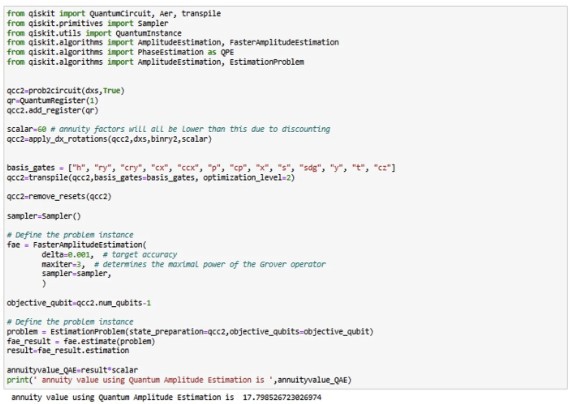
Актуарын математикийг квантжуулах
Квант тооцоолол нь үнэ тогтоох, нөөц сан тооцоолох, эрсдэлийн загварчлал хийх зэрэгт цоо шинэ хандлагыг санал болгож чадна. Томоохон өгөгдлийн багцыг(entire life table) цөөн кубитэд кодлох замаар актуариуд асар бага нөөц ашиглан онолын хувьд тооцоо хийх боломжтой. Хэдийгээр бодит квант компьютерууд одоогоор дутагдалтай байдал ихтэй хэвээр байгаа ч, квант аргыг актуарын ажлыг хялбарчлах, сайжруулахад хэрхэн ашиглаж болохыг судлах ойлголт, хэрэгслүүд аль хэдийн бий болсон.
Суперпозици, энтанглемент болон квант схемийн энэхүү товчхон танилцуулга нь эдгээр технологи бүрэн боловсорсон үед загварчлалын ажлыг хурдасгаж, эрсдэл ба тодорхойгүй байдлын талаарх шинэ ойлголтыг нээж болохыг харуулж байна. Актуарын ур чадвараа квантжуулахыг хүсэж байвал дараах дөрвөн алхмыг хийгээрэй:
Хамгийн гол нь нээлттэй сэтгэлгээтэй байх. Квант логикийн онцлогийг хүлээн зөвшөөрч, энэхүү шинэ ертөнцийг сонирхон судалж, өөрийн ур чадвараа жинхэнэ утгаар нь дараагийн түвшинд хүргэх боломжийг ашиглаарай.
Мэдээ бэлтгэсэн: Математикийн салбар, ЭШДэА, Г.Гантигмаа
Эх сурвалж: Mass Appeal: How quantum computing can be applied to life insurance, Muhammad Amjad, May/June 2025, The Actuary Magazine